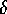 . If
. If 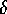 is large enough (in particular in relation to
is large enough (in particular in relation to 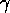 )
and
)
and 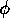 , this results in an action selection that protects
protected global goals.
, this results in an action selection that protects
protected global goals.



A bad ordering of actions can dramatically increase the number of actions
necessary to achieve a goal, or even prevent a solution from ever being
found. Any action selection algorithm should therefore to some degree be able to
arbitrate among conflicting actions. Our algorithm is able to do so because
of the inhibition rules. The modules in a network that undo a
protected goal are weakened by a factor of 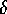 . If
. If 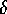 is large enough (in particular in relation to
is large enough (in particular in relation to 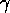 )
and
)
and 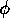 , this results in an action selection that protects
protected global goals.
, this results in an action selection that protects
protected global goals.
The same is true for subgoals (or preconditions of modules). Every module
decreases the activation level of modules that undo its true conditions.
Again this results in an action selection behavior in which `subgoals' are
protected and thereby goal conflicts are avoided. To illustrate how this
happens, we reimplemented the classical anomalous situation example of the
blocks world (Sussman, 1975). Figure  illustrates the problem.
Figure
illustrates the problem.
Figure  shows some of the competence modules involved in this example.
shows some of the competence modules involved in this example.
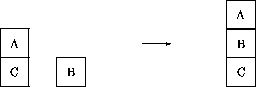
Figure: The classical conflicting goals example.
The initial state of the world is S(0)=(clear-a, clear-b, a-on-c), the goals are G(0)=(a-on-b, b-on-c).
The system should
first achieve the goal b-on-c and then the goal a-on-b. It is tempted
however to immediately stack a onto b, which may bring it in a deadlock
situation (not wanting to undo the already achieved goal).

Figure: Some of the modules involved in the blocks world domain.
Figure  and
and  show the results obtained. In the first experiment
show the results obtained. In the first experiment
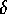 has the same value as
has the same value as 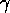 which is far
greater than
which is far
greater than 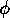 . The result is that the inhibition of
`stack-a-on-b' by `stack-b-on-c' for condition `clear-b' is far more
important than its activation by the state. Because of this, the module
`take-a-from-b' dominates over `stack-a-on-b', despite the fact that the
latter one achieves a goal. If
. The result is that the inhibition of
`stack-a-on-b' by `stack-b-on-c' for condition `clear-b' is far more
important than its activation by the state. Because of this, the module
`take-a-from-b' dominates over `stack-a-on-b', despite the fact that the
latter one achieves a goal. If 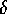 is not high enough (as
in the second experiment), the urge to fulfill the goal `a-on-b'
dominates over the urge to avoid `clear-b', so that the system does take off by
stacking a on b. It is however still able to restore the situation and
obtain the two goals, since the influence from the protected goals is not
high enough to keep the system from undoing the achieved goal `a-on-b'.
Again, a balance has to be found between not caring about goal
conflicts at all and being so rigid as to never undo an achieved (sub-) goal,
thereby risking deadlocks.
is not high enough (as
in the second experiment), the urge to fulfill the goal `a-on-b'
dominates over the urge to avoid `clear-b', so that the system does take off by
stacking a on b. It is however still able to restore the situation and
obtain the two goals, since the influence from the protected goals is not
high enough to keep the system from undoing the achieved goal `a-on-b'.
Again, a balance has to be found between not caring about goal
conflicts at all and being so rigid as to never undo an achieved (sub-) goal,
thereby risking deadlocks.

Figure: When the influence from protected goals and the
threshold are high enough, the system is able to avoid problems with
conflicting goals.

Figure: In both these experiments the system reacts opportunistically,
not taking into account conflicting goals. In the first experiment, the
parameter 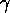 is low, so that the system is not very sensitive to
goal-conflicts. In the second experiment, the threshold is not high enough,
so that the system chooses a local maximum.
is low, so that the system is not very sensitive to
goal-conflicts. In the second experiment, the threshold is not high enough,
so that the system chooses a local maximum.


