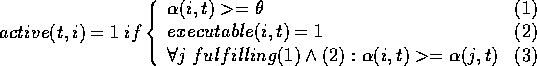Next: Example
Up: HOW TO DO THE
Previous: Algorithm
This section of the paper presents a mathematical description of the algorithm so as to
make reproduction of the results possible. Given:
- a set of competence modules
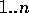 ,
,
- a set of propositions
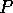 ,
,
- a function
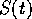 returning the propositions that are
observed to be true at time
returning the propositions that are
observed to be true at time 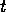 (the state of the environment as
perceived by the agent);
(the state of the environment as
perceived by the agent); 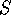 being implemented by an
independent process (or the real world),
being implemented by an
independent process (or the real world),
- a function
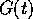 returning the propositions that are a goal
of the agent at time
returning the propositions that are a goal
of the agent at time 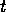 ;
;
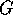 being implemented by an independent process,
being implemented by an independent process,
- a function
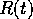 returning the propositions that are a goal
of the agent that has already been achieved at time
returning the propositions that are a goal
of the agent that has already been achieved at time 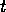 ;
; 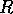 being implemented by
an independent process (e.g. some internal or external goal creator),
being implemented by
an independent process (e.g. some internal or external goal creator),
- a function
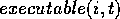 , which returns 1 if competence
module
, which returns 1 if competence
module 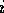 is executable at time
is executable at time 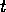 (i.e., if all of the preconditions
of competence module
(i.e., if all of the preconditions
of competence module 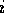 are members of
are members of 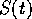 ),
and 0 otherwise.
),
and 0 otherwise.
- a function
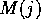 , which returns the set of modules that match
proposition
, which returns the set of modules that match
proposition 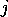 , i.e., the modules
, i.e., the modules  for which
for which 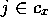 ,
,
- a function
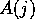 , which returns the set of modules that
achieve proposition
, which returns the set of modules that
achieve proposition 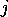 , i.e., the modules
, i.e., the modules  for which
for which 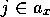 ,
,
- a function
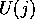 , which returns the set of modules that undo
proposition
, which returns the set of modules that undo
proposition 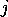 , i.e., the modules
, i.e., the modules  for which
for which 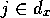 ,
,
 , the mean level of activation,
, the mean level of activation,
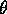 , the threshold of activation, where
, the threshold of activation, where 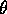 is lowered 10% every time no module could be selected, and is reset to
its initial value whenever a module becomes active.
is lowered 10% every time no module could be selected, and is reset to
its initial value whenever a module becomes active.
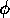 , the amount of activation energy injected by the state per true
proposition,
, the amount of activation energy injected by the state per true
proposition,
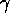 , the amount of activation energy injected by the goals per goal,
, the amount of activation energy injected by the goals per goal,
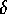 , the amount of activation energy taken away by the protected goals per protected goal.
, the amount of activation energy taken away by the protected goals per protected goal.
Given competence module 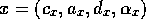 ,
the input of activation to module
,
the input of activation to module  from the
state at time
from the
state at time 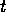 is:
is:

where 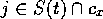 and where
and where
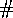 stands for the cardinality of a set.
stands for the cardinality of a set.
The input of activation to competence module  from the goals at
time
from the goals at
time 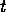 is:
is:
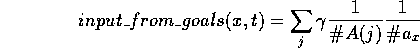
where 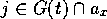 .
.
The removal of activation from competence module  by the
goals that are protected at time
by the
goals that are protected at time 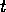 is:
is:
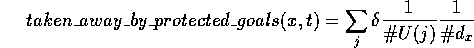
where 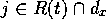 .
.
The following equation specifies what a competence module
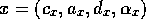 spreads
backward to a competence
module
spreads
backward to a competence
module 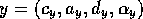 :
:
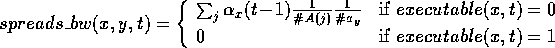
where 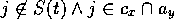 .
.
The following equation specifies what module  spreads forward to module
spreads forward to module 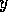 :
:
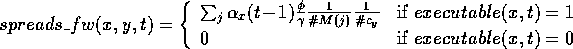
where 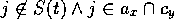 .
.
The following equation specifies what module  takes away from module
takes away from module 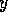 :
:
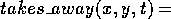
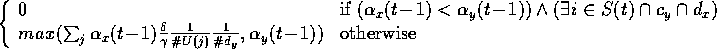
where 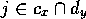 .
.
The activation level of a competence module 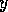 at time
at time 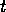 is defined as:
is defined as:
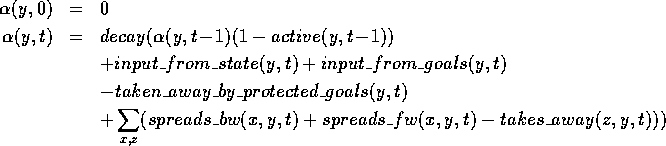
where  ranges over the modules of the network,
ranges over the modules of the network,
 ranges over the modules of the network minus the module
ranges over the modules of the network minus the module
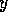 ,
,
 , and the decay function is such that the global
activation remains constant:
, and the decay function is such that the global
activation remains constant:

The competence module that becomes active at time 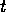 is module
is module 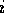 such that:
such that:
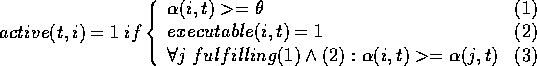
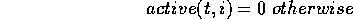



Next: Example
Up: HOW TO DO THE
Previous: Algorithm
Alexandros Moukas
Wed Feb 7 14:24:19 EST 1996
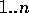 ,
,
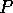 ,
,
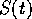 returning the propositions that are
observed to be true at time
returning the propositions that are
observed to be true at time 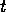 (the state of the environment as
perceived by the agent);
(the state of the environment as
perceived by the agent); 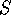 being implemented by an
independent process (or the real world),
being implemented by an
independent process (or the real world),
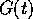 returning the propositions that are a goal
of the agent at time
returning the propositions that are a goal
of the agent at time 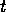 ;
;
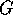 being implemented by an independent process,
being implemented by an independent process,
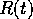 returning the propositions that are a goal
of the agent that has already been achieved at time
returning the propositions that are a goal
of the agent that has already been achieved at time 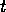 ;
; 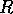 being implemented by
an independent process (e.g. some internal or external goal creator),
being implemented by
an independent process (e.g. some internal or external goal creator),
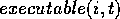 , which returns 1 if competence
module
, which returns 1 if competence
module 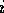 is executable at time
is executable at time 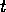 (i.e., if all of the preconditions
of competence module
(i.e., if all of the preconditions
of competence module 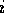 are members of
are members of 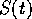 ),
and 0 otherwise.
),
and 0 otherwise.
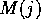 , which returns the set of modules that match
proposition
, which returns the set of modules that match
proposition 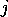 , i.e., the modules
, i.e., the modules  for which
for which 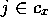 ,
,
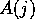 , which returns the set of modules that
achieve proposition
, which returns the set of modules that
achieve proposition 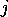 , i.e., the modules
, i.e., the modules  for which
for which 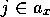 ,
,
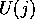 , which returns the set of modules that undo
proposition
, which returns the set of modules that undo
proposition 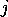 , i.e., the modules
, i.e., the modules  for which
for which 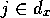 ,
,
 , the mean level of activation,
, the mean level of activation,
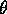 , the threshold of activation, where
, the threshold of activation, where 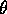 is lowered 10% every time no module could be selected, and is reset to
its initial value whenever a module becomes active.
is lowered 10% every time no module could be selected, and is reset to
its initial value whenever a module becomes active.
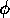 , the amount of activation energy injected by the state per true
proposition,
, the amount of activation energy injected by the state per true
proposition,
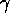 , the amount of activation energy injected by the goals per goal,
, the amount of activation energy injected by the goals per goal,
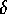 , the amount of activation energy taken away by the protected goals per protected goal.
, the amount of activation energy taken away by the protected goals per protected goal.



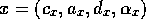 ,
the input of activation to module
,
the input of activation to module  from the
state at time
from the
state at time 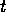 is:
is:

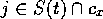 and where
and where
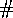 stands for the cardinality of a set.
stands for the cardinality of a set.
 from the goals at
time
from the goals at
time  is:
is:
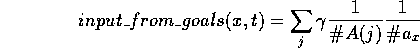
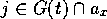 .
.
 by the
goals that are protected at time
by the
goals that are protected at time 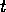 is:
is:
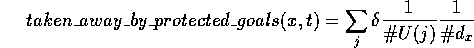
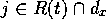 .
.
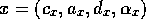 spreads
backward to a competence
module
spreads
backward to a competence
module 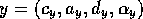 :
:
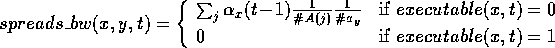
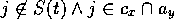 .
.
 spreads forward to module
spreads forward to module 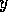 :
:
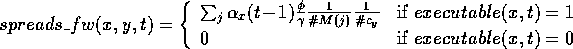
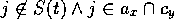 .
.
 takes away from module
takes away from module 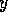 :
:
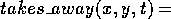
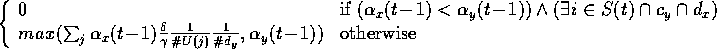
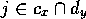 .
.
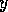 at time
at time 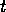 is defined as:
is defined as:
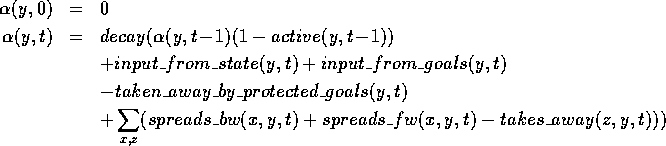
 ranges over the modules of the network,
ranges over the modules of the network,
 ranges over the modules of the network minus the module
ranges over the modules of the network minus the module
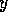 ,
,
 , and the decay function is such that the global
activation remains constant:
, and the decay function is such that the global
activation remains constant:

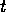 is module
is module 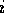 such that:
such that: