


Next: Mathematical Model
Up: HOW TO DO THE
Previous: Introduction
An autonomous agent is viewed as a set of competence modules. These
competence modules resemble the operators of a classical planning system. A
competence module 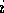 can be described by a tuple
can be described by a tuple 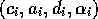 .
. 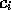 is a list of preconditions which have to be fulfilled before the competence
module can become active.
is a list of preconditions which have to be fulfilled before the competence
module can become active. 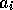 and
and 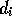 represent the expected effects of the competence module's action in terms of
an add list and a delete list. In addition, each competence module has a
level of activation
represent the expected effects of the competence module's action in terms of
an add list and a delete list. In addition, each competence module has a
level of activation 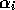 . A competence module is
executable at time
. A competence module is
executable at time 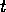 when all of its preconditions are observed to be
true at time t. An executable competence module may be selected, which
means that it performs some real world actions. The operation of a
competence module (what computation it performs, what actions it takes and
how) is not made explicit, i.e., competence modules could be hard-wired
inside, they could perform logical inference, or whatever.
when all of its preconditions are observed to be
true at time t. An executable competence module may be selected, which
means that it performs some real world actions. The operation of a
competence module (what computation it performs, what actions it takes and
how) is not made explicit, i.e., competence modules could be hard-wired
inside, they could perform logical inference, or whatever.
Competence modules are linked in a network through three types of links:
successor links, predecessor links, and conflicter links. The description
of the competence modules of a autonomous agent in terms of a precondition list, add
list and delete list completely defines this network:
The intuitive idea is that modules use these links to activate and inhibit
each other, so that after some time the activation energy accumulates in the
modules that represent the `best' actions to take given the current
situation and goals. Once the activation level of such a module surpasses a
certain threshold, and provided the module is executable, it becomes active and takes some real actions.
The pattern of spreading activation among modules, as well as the input of
new activation energy into the network is determined by the current state of
the environment and the current global goals of the agent:
- Activation by the State
There is input of activation energy coming from the state of the environment
towards modules that partially match the current state. A competence
module is said to partially match the current state if at least one of its
preconditions is observed to be true.
- Activation by the Goals
A second source of activation energy is the global goals of the agent.
They increase the activation level of modules that achieve one of the
global goals. A module is said to achieve one of the global goals if one of
the goals is a member of the add list of the competence module. Notice that we
distinguish two types of goals: once-only goals have to be achieved
only once, permanent goals have to be achieved continuously. An
example of the first is the goal `spray-paint-car', an example of the
second would be `no-self-damage'.
- Inhibition by the Protected Goals
Further, there is an external inhibition (or removal of activation) by the
global goals of the agent that have already been achieved and should be protected. These `protected goals'
remove some of the activation from the modules that would undo them.
A module is said to undo one of the protected goals when one
of the protected goals is member of the delete list of the module.
These processes are continuous: there is a continual flow of activation
energy towards the modules that partially match the current state and
towards the modules that realize one of the global goals. There is a
continual decrease of the activation level of the modules that undo the
protected goals. This means that the state of the environment and the global
goals may change unpredictably at any moment in time. If this happens, the
external input of activation automatically flows to other competence
modules.
Besides the impact on activation levels from the state and goals, competence
modules also activate and inhibit each other. Modules spread activation
along their links as follows:
- Activation of Successors
An executable competence module  spreads activation forward. It
increases (by a fraction of
its own activation level) the activation level of those successors
spreads activation forward. It
increases (by a fraction of
its own activation level) the activation level of those successors 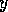 for which the shared
proposition
for which the shared
proposition 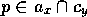 is not true. Intuitively, we want these successor
modules to become more activated because they are `almost executable', since
more of their preconditions will be fulfilled after the competence module has
become active. Formally, given that competence
module
is not true. Intuitively, we want these successor
modules to become more activated because they are `almost executable', since
more of their preconditions will be fulfilled after the competence module has
become active. Formally, given that competence
module 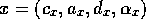 is
executable, it spreads forward through those
successor links for which the
proposition that defines them
is
executable, it spreads forward through those
successor links for which the
proposition that defines them 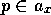 is
false.
is
false.
- Activation of Predecessors
A competence module  that is not executable spreads activation backward.
It increases (by a fraction of
its own activation level) the activation level of those predecessors
that is not executable spreads activation backward.
It increases (by a fraction of
its own activation level) the activation level of those predecessors 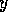 for which the
shared proposition
for which the
shared proposition 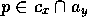 is not true.
Intuitively, a non-executable competence module spreads
to the modules that `promise' to fulfill its preconditions that are
not yet true, so that the competence module may become
executable afterwards. Formally, given that competence
module
is not true.
Intuitively, a non-executable competence module spreads
to the modules that `promise' to fulfill its preconditions that are
not yet true, so that the competence module may become
executable afterwards. Formally, given that competence
module 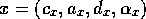 is not executable, it spreads backward through those predecessor links for
which the proposition that defined them
is not executable, it spreads backward through those predecessor links for
which the proposition that defined them 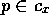 is false.
is false.
- Inhibition of Conflicters
Every competence module  (executable or not) decreases
(by a fraction
of its own activation level) the activation level
of those conflicters
(executable or not) decreases
(by a fraction
of its own activation level) the activation level
of those conflicters 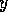 for which the shared proposition
for which the shared proposition 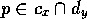 is true.
Intuitively, a module tries to prevent a module that undoes its
true preconditions from becoming active. Notice that we do not allow a module to
inhibit itself (while it may activate itself). In case of mutual conflict
of modules, only the one with the highest activation level inhibits the
other. This prevents the phenomenon that the most relevant
modules eliminate each other. Formally, competence module
is true.
Intuitively, a module tries to prevent a module that undoes its
true preconditions from becoming active. Notice that we do not allow a module to
inhibit itself (while it may activate itself). In case of mutual conflict
of modules, only the one with the highest activation level inhibits the
other. This prevents the phenomenon that the most relevant
modules eliminate each other. Formally, competence module
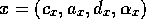 takes
away activation energy through all of its conflicter links for which the
proposition that defines them
takes
away activation energy through all of its conflicter links for which the
proposition that defines them 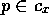 is
true, except those links for which there exists an inverse conflicter link that is
stronger.
is
true, except those links for which there exists an inverse conflicter link that is
stronger.
The global algorithm performs a loop, in which at every timestep the
following computation takes place over all of the competence modules:
- The impact of the state, goals and protected goals on the activation level of a module is
computed.
- The way the competence module activates and inhibits related
modules through its successor links, predecessor links and conflicter links is computed.
- A decay function ensures that the overall activation level remains
constant.
- The competence module that fulfills the following three conditions
becomes active: (i) It has to be executable, (ii) Its
level of activation has to surpass a certain threshold and (iii) It must
have a higher activation level than all other competence modules that
fulfill conditions (i) and (ii).
When two competence modules fulfill these
conditions (i.e., they are equally strong), one of them is chosen randomly.
The activation level of the module that has become active is reinitialized to
0
 . If none of the modules
fulfills conditions (i) and (ii), the threshold is lowered by 10%.
. If none of the modules
fulfills conditions (i) and (ii), the threshold is lowered by 10%.
These four steps are repeated infinitely. Interesting global observable
properties are: the sequence of competence modules that have become active,
the optimality of this sequence (which is computed by a domain-dependent
function), and the speed with which it was obtained (the number of timesteps a
competence module has become active relative to the total number of
timesteps the system has been running).
Four global parameters can be used to `tune' the spreading activation
dynamics, and thereby the action selection behavior of the agent:
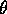 , the threshold for becoming active, and related to
it,
, the threshold for becoming active, and related to
it,  the mean level of activation.
the mean level of activation.
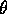 is lowered with 10% each time none of the modules could
be selected. It is reset to its initial value when a module could be selected.
is lowered with 10% each time none of the modules could
be selected. It is reset to its initial value when a module could be selected.
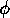 , the amount of activation energy a proposition that
is observed to be true injects into the network.
, the amount of activation energy a proposition that
is observed to be true injects into the network.
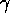 , the amount of activation energy a goal
injects into the network.
, the amount of activation energy a goal
injects into the network.
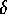 , the amount of activation energy a protected goal
takes away from the network.
, the amount of activation energy a protected goal
takes away from the network.
These parameters also determine the amount of activation that modules spread
forward, backward or take away. More precisely, per false proposition in its
precondition list, a non-executable module spreads 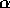 to its predecessors.
Per false proposition in its add list, an executable module spreads
to its predecessors.
Per false proposition in its add list, an executable module spreads
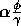 to its successors. Per true proposition in its precondition list a
module takes away
to its successors. Per true proposition in its precondition list a
module takes away 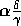 from its conflictors. These
factors were chosen this way because the internal spreading of activation should have
the same semantics/effects as the input/output by the state and the goals.
The ratios of input from the state versus input from the goals
versus output by the protected goals are the same as the ratios of input from
predecessors versus input from successors versus output by modules with
which a module conflicts.
Intuitively, we want to view preconditions that are not yet true as subgoals,
effects that are about to be true as `predictions', and preconditions that
are true as protected subgoals.
from its conflictors. These
factors were chosen this way because the internal spreading of activation should have
the same semantics/effects as the input/output by the state and the goals.
The ratios of input from the state versus input from the goals
versus output by the protected goals are the same as the ratios of input from
predecessors versus input from successors versus output by modules with
which a module conflicts.
Intuitively, we want to view preconditions that are not yet true as subgoals,
effects that are about to be true as `predictions', and preconditions that
are true as protected subgoals.
The algorithm as it is described until now, has some drawback that has
to be dealt with.
The length of a precondition list, add
list or delete list affects the input and output of activation
to a module. In particular, a module which has a lot of propositions in
its add list and precondition list, has more sources of
activation energy than a module that only has a few.
Therefore, all input of activation to a module or removal of activation from a
module is weighted by 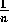 , where
, where  is (i)
the number of propositions in the precondition list (in the case of input
coming from the state and from the predecessors), (ii) the number of
preconditions in the add-list (in the case of input from the goals or from
successors), or (iii) the number of propositions in the delete list (in the
case of removal of activation by the protected goals or by modules with whom
the module conflicts).
is (i)
the number of propositions in the precondition list (in the case of input
coming from the state and from the predecessors), (ii) the number of
preconditions in the add-list (in the case of input from the goals or from
successors), or (iii) the number of propositions in the delete list (in the
case of removal of activation by the protected goals or by modules with whom
the module conflicts).
Finally, we want modules that achieve the same goal or modules that
use the same precondition to compete with one another to become active
(we view them as representing a disjunction or choice point). Therefore,
the amount of activation that is spread or taken away for a
particular proposition is split among the affected modules. For example, for
a particular proposition 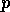 that is observed to be true the state divides
that is observed to be true the state divides
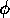 among all of the modules that have that precondition in their
precondition list. The same not only holds for the effect of the goals and the
protected goals, but also for the internal spreading of activation. For
example when a large number of modules achieve a precondition of module m,
the activation
among all of the modules that have that precondition in their
precondition list. The same not only holds for the effect of the goals and the
protected goals, but also for the internal spreading of activation. For
example when a large number of modules achieve a precondition of module m,
the activation 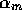 that
that 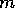 spreads backward for
that proposition is equally divided among all of these modules. When on
the other hand there is only one other module that can make this precondition
true, module
spreads backward for
that proposition is equally divided among all of these modules. When on
the other hand there is only one other module that can make this precondition
true, module 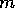 increases the activation level of that module by its own
activation level
increases the activation level of that module by its own
activation level 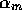 . One implicit assumption on
which this is based is that the preconditions are in conjunctive normal form.
A disjunction of two preconditions would be represented by a single
proposition, for which two competence modules exist that can make it true.
. One implicit assumption on
which this is based is that the preconditions are in conjunctive normal form.
A disjunction of two preconditions would be represented by a single
proposition, for which two competence modules exist that can make it true.



Next: Mathematical Model
Up: HOW TO DO THE
Previous: Introduction
Alexandros Moukas
Wed Feb 7 14:24:19 EST 1996
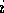 can be described by a tuple
can be described by a tuple 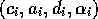 .
. 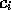 is a list of preconditions which have to be fulfilled before the competence
module can become active.
is a list of preconditions which have to be fulfilled before the competence
module can become active. 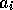 and
and 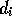 represent the expected effects of the competence module's action in terms of
an add list and a delete list. In addition, each competence module has a
level of activation
represent the expected effects of the competence module's action in terms of
an add list and a delete list. In addition, each competence module has a
level of activation 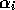 . A competence module is
executable at time
. A competence module is
executable at time 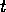 when all of its preconditions are observed to be
true at time t. An executable competence module may be selected, which
means that it performs some real world actions. The operation of a
competence module (what computation it performs, what actions it takes and
how) is not made explicit, i.e., competence modules could be hard-wired
inside, they could perform logical inference, or whatever.
when all of its preconditions are observed to be
true at time t. An executable competence module may be selected, which
means that it performs some real world actions. The operation of a
competence module (what computation it performs, what actions it takes and
how) is not made explicit, i.e., competence modules could be hard-wired
inside, they could perform logical inference, or whatever.



 to competence
module
to competence
module 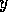 (`
(` has
has 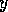 as successor') for every proposition
as successor') for every proposition  that is member of
the add list of
that is member of
the add list of  and also member of the precondition list of
and also member of the precondition list of 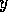 (so more than
one successor link between two competence modules may exist). Formally,
given competence module
(so more than
one successor link between two competence modules may exist). Formally,
given competence module 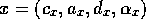 and competence module
and competence module 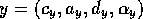 ,
there is a successor link from
,
there is a successor link from  to y, for every
proposition
to y, for every
proposition 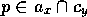 .
.
 to module
to module 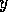 (`
(` has
has 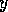 as predecessor') exists
for every successor link from
as predecessor') exists
for every successor link from 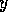 to
to  . Formally, given
competence module
. Formally, given
competence module 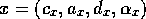 and competence module
and competence module 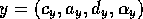 ,
there is a predecessor
link from
,
there is a predecessor
link from  to y, for every proposition
to y, for every proposition 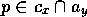 .
.
 to module
to module 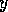 (`
(`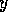 conflicts with
x') for every proposition
conflicts with
x') for every proposition 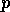 that is a member of the delete list of
that is a member of the delete list of 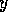 and a
member of the precondition list of
and a
member of the precondition list of  . Formally, given competence
module
. Formally, given competence
module 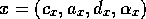 and
competence module
and
competence module 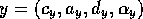 ,
there is a conflicter link from
,
there is a conflicter link from  to y, for every
proposition
to y, for every
proposition 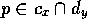 .
.
 spreads activation forward. It
increases (by a fraction of
its own activation level) the activation level of those successors
spreads activation forward. It
increases (by a fraction of
its own activation level) the activation level of those successors 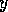 for which the shared
proposition
for which the shared
proposition 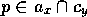 is not true. Intuitively, we want these successor
modules to become more activated because they are `almost executable', since
more of their preconditions will be fulfilled after the competence module has
become active. Formally, given that competence
module
is not true. Intuitively, we want these successor
modules to become more activated because they are `almost executable', since
more of their preconditions will be fulfilled after the competence module has
become active. Formally, given that competence
module 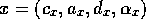 is
executable, it spreads forward through those
successor links for which the
proposition that defines them
is
executable, it spreads forward through those
successor links for which the
proposition that defines them 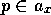 is
false.
is
false.
 that is not executable spreads activation backward.
It increases (by a fraction of
its own activation level) the activation level of those predecessors
that is not executable spreads activation backward.
It increases (by a fraction of
its own activation level) the activation level of those predecessors 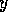 for which the
shared proposition
for which the
shared proposition 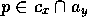 is not true.
Intuitively, a non-executable competence module spreads
to the modules that `promise' to fulfill its preconditions that are
not yet true, so that the competence module may become
executable afterwards. Formally, given that competence
module
is not true.
Intuitively, a non-executable competence module spreads
to the modules that `promise' to fulfill its preconditions that are
not yet true, so that the competence module may become
executable afterwards. Formally, given that competence
module 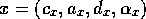 is not executable, it spreads backward through those predecessor links for
which the proposition that defined them
is not executable, it spreads backward through those predecessor links for
which the proposition that defined them 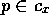 is false.
is false.
 (executable or not) decreases
(by a fraction
of its own activation level) the activation level
of those conflicters
(executable or not) decreases
(by a fraction
of its own activation level) the activation level
of those conflicters 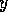 for which the shared proposition
for which the shared proposition 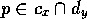 is true.
Intuitively, a module tries to prevent a module that undoes its
true preconditions from becoming active. Notice that we do not allow a module to
inhibit itself (while it may activate itself). In case of mutual conflict
of modules, only the one with the highest activation level inhibits the
other. This prevents the phenomenon that the most relevant
modules eliminate each other. Formally, competence module
is true.
Intuitively, a module tries to prevent a module that undoes its
true preconditions from becoming active. Notice that we do not allow a module to
inhibit itself (while it may activate itself). In case of mutual conflict
of modules, only the one with the highest activation level inhibits the
other. This prevents the phenomenon that the most relevant
modules eliminate each other. Formally, competence module
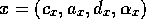 takes
away activation energy through all of its conflicter links for which the
proposition that defines them
takes
away activation energy through all of its conflicter links for which the
proposition that defines them 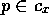 is
true, except those links for which there exists an inverse conflicter link that is
stronger.
is
true, except those links for which there exists an inverse conflicter link that is
stronger.

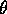 , the threshold for becoming active, and related to
it,
, the threshold for becoming active, and related to
it,  the mean level of activation.
the mean level of activation.
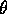 is lowered with 10% each time none of the modules could
be selected. It is reset to its initial value when a module could be selected.
is lowered with 10% each time none of the modules could
be selected. It is reset to its initial value when a module could be selected.
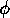 , the amount of activation energy a proposition that
is observed to be true injects into the network.
, the amount of activation energy a proposition that
is observed to be true injects into the network.
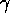 , the amount of activation energy a goal
injects into the network.
, the amount of activation energy a goal
injects into the network.
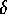 , the amount of activation energy a protected goal
takes away from the network.
, the amount of activation energy a protected goal
takes away from the network.
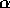 to its predecessors.
Per false proposition in its add list, an executable module spreads
to its predecessors.
Per false proposition in its add list, an executable module spreads
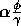 to its successors. Per true proposition in its precondition list a
module takes away
to its successors. Per true proposition in its precondition list a
module takes away 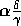 from its conflictors. These
factors were chosen this way because the internal spreading of activation should have
the same semantics/effects as the input/output by the state and the goals.
The ratios of input from the state versus input from the goals
versus output by the protected goals are the same as the ratios of input from
predecessors versus input from successors versus output by modules with
which a module conflicts.
Intuitively, we want to view preconditions that are not yet true as subgoals,
effects that are about to be true as `predictions', and preconditions that
are true as protected subgoals.
from its conflictors. These
factors were chosen this way because the internal spreading of activation should have
the same semantics/effects as the input/output by the state and the goals.
The ratios of input from the state versus input from the goals
versus output by the protected goals are the same as the ratios of input from
predecessors versus input from successors versus output by modules with
which a module conflicts.
Intuitively, we want to view preconditions that are not yet true as subgoals,
effects that are about to be true as `predictions', and preconditions that
are true as protected subgoals.
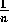 , where
, where  is (i)
the number of propositions in the precondition list (in the case of input
coming from the state and from the predecessors), (ii) the number of
preconditions in the add-list (in the case of input from the goals or from
successors), or (iii) the number of propositions in the delete list (in the
case of removal of activation by the protected goals or by modules with whom
the module conflicts).
is (i)
the number of propositions in the precondition list (in the case of input
coming from the state and from the predecessors), (ii) the number of
preconditions in the add-list (in the case of input from the goals or from
successors), or (iii) the number of propositions in the delete list (in the
case of removal of activation by the protected goals or by modules with whom
the module conflicts).
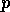 that is observed to be true the state divides
that is observed to be true the state divides
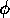 among all of the modules that have that precondition in their
precondition list. The same not only holds for the effect of the goals and the
protected goals, but also for the internal spreading of activation. For
example when a large number of modules achieve a precondition of module m,
the activation
among all of the modules that have that precondition in their
precondition list. The same not only holds for the effect of the goals and the
protected goals, but also for the internal spreading of activation. For
example when a large number of modules achieve a precondition of module m,
the activation 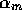 that
that 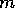 spreads backward for
that proposition is equally divided among all of these modules. When on
the other hand there is only one other module that can make this precondition
true, module
spreads backward for
that proposition is equally divided among all of these modules. When on
the other hand there is only one other module that can make this precondition
true, module 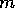 increases the activation level of that module by its own
activation level
increases the activation level of that module by its own
activation level 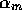 . One implicit assumption on
which this is based is that the preconditions are in conjunctive normal form.
A disjunction of two preconditions would be represented by a single
proposition, for which two competence modules exist that can make it true.
. One implicit assumption on
which this is based is that the preconditions are in conjunctive normal form.
A disjunction of two preconditions would be represented by a single
proposition, for which two competence modules exist that can make it true.