


Next: Situation Relevance
Up: Results
Previous: Results
The algorithm selects actions that contribute to the global goals of the
agent. Given that 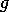 is a global goal of the network, then
is a global goal of the network, then
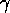 of new activation energy is put into the modules
that achieve this goal. These modules will in turn per subgoal (false precondition) increase the activation level of the modules
that make this subgoal true, and so on. This backward spreading of
activation takes care that modules that contribute to goal
of new activation energy is put into the modules
that achieve this goal. These modules will in turn per subgoal (false precondition) increase the activation level of the modules
that make this subgoal true, and so on. This backward spreading of
activation takes care that modules that contribute to goal 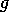 are more activated than modules that don't. Furthermore modules that contribute to different goals (or subgoals) receive activation
for each of these goals and will therefore be favored over modules that only contribute to one.
are more activated than modules that don't. Furthermore modules that contribute to different goals (or subgoals) receive activation
for each of these goals and will therefore be favored over modules that only contribute to one.
If the agent has more than one goal, modules that contribute to the goal
that is `closest' are favored. `Closest' here means that the path from
the goal-achieving modules to the state-matching modules is the shortest.
The algorithm also favors modules that have little competition. For example, if the
agent has two goals 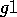 and
and 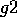 and if there
is one module that achieves
and if there
is one module that achieves 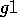 and there are two modules
that achieve
and there are two modules
that achieve 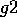 then the algorithm favors the module
that achieves
then the algorithm favors the module
that achieves 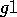 , and therefore the probability of
, and therefore the probability of 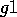 being realized first is higher. All of these comments hold
for subgoals as well as for goals, since subgoals (false preconditions
of modules) are treated the same way as goals.
being realized first is higher. All of these comments hold
for subgoals as well as for goals, since subgoals (false preconditions
of modules) are treated the same way as goals.
The behavior can be made more or less goal-oriented in its selection
by varying the ratio of 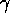 to
to 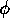 (the amount of activation energy injected by the state per true proposition).
For example, if
(the amount of activation energy injected by the state per true proposition).
For example, if 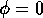 , traditional backward chaining is performed
(i.e., the selection is completely goal-oriented). On the other hand, the
system now takes less advantage of opportunities, it is less
reactive. Furthermore, it is also slowed down because the current state
of the environment does not bias the action selection. Ideally we want a
system that is mainly goal-oriented, but does take advantage of
interesting opportunities. This can be obtained by choosing
, traditional backward chaining is performed
(i.e., the selection is completely goal-oriented). On the other hand, the
system now takes less advantage of opportunities, it is less
reactive. Furthermore, it is also slowed down because the current state
of the environment does not bias the action selection. Ideally we want a
system that is mainly goal-oriented, but does take advantage of
interesting opportunities. This can be obtained by choosing 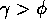 . The optimal ratio is of course problem dependent (more on choosing the parameter values in section 6.4).
. The optimal ratio is of course problem dependent (more on choosing the parameter values in section 6.4).



Next: Situation Relevance
Up: Results
Previous: Results
Alexandros Moukas
Wed Feb 7 14:24:19 EST 1996
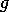 is a global goal of the network, then
is a global goal of the network, then
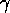 of new activation energy is put into the modules
that achieve this goal. These modules will in turn per subgoal (false precondition) increase the activation level of the modules
that make this subgoal true, and so on. This backward spreading of
activation takes care that modules that contribute to goal
of new activation energy is put into the modules
that achieve this goal. These modules will in turn per subgoal (false precondition) increase the activation level of the modules
that make this subgoal true, and so on. This backward spreading of
activation takes care that modules that contribute to goal 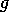 are more activated than modules that don't. Furthermore modules that contribute to different goals (or subgoals) receive activation
for each of these goals and will therefore be favored over modules that only contribute to one.
are more activated than modules that don't. Furthermore modules that contribute to different goals (or subgoals) receive activation
for each of these goals and will therefore be favored over modules that only contribute to one.



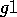 and
and 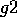 and if there
is one module that achieves
and if there
is one module that achieves 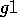 and there are two modules
that achieve
and there are two modules
that achieve 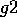 then the algorithm favors the module
that achieves
then the algorithm favors the module
that achieves 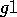 , and therefore the probability of
, and therefore the probability of 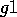 being realized first is higher. All of these comments hold
for subgoals as well as for goals, since subgoals (false preconditions
of modules) are treated the same way as goals.
being realized first is higher. All of these comments hold
for subgoals as well as for goals, since subgoals (false preconditions
of modules) are treated the same way as goals.
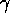 to
to 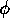 (the amount of activation energy injected by the state per true proposition).
For example, if
(the amount of activation energy injected by the state per true proposition).
For example, if 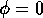 , traditional backward chaining is performed
(i.e., the selection is completely goal-oriented). On the other hand, the
system now takes less advantage of opportunities, it is less
reactive. Furthermore, it is also slowed down because the current state
of the environment does not bias the action selection. Ideally we want a
system that is mainly goal-oriented, but does take advantage of
interesting opportunities. This can be obtained by choosing
, traditional backward chaining is performed
(i.e., the selection is completely goal-oriented). On the other hand, the
system now takes less advantage of opportunities, it is less
reactive. Furthermore, it is also slowed down because the current state
of the environment does not bias the action selection. Ideally we want a
system that is mainly goal-oriented, but does take advantage of
interesting opportunities. This can be obtained by choosing 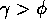 . The optimal ratio is of course problem dependent (more on choosing the parameter values in section 6.4).
. The optimal ratio is of course problem dependent (more on choosing the parameter values in section 6.4).